The best option to understand what Knowledge Representation is simply to mention what it is intended for. Its mission is to make knowledge as explicit as possible. This is necessary because knowledge is stored in implicit form, i.e. tacit knowledge non-observable from the outside, inside minds and spread around in community social habits. To facilitate knowledge sharing it is necessary to make it explicit.
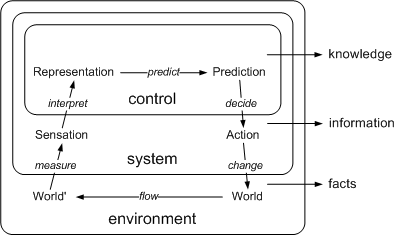
Tacit knowledge is what an agent obtains when it observes its environment and makes internal representations of what it perceives. Here "agent" stands for an entity capable of election. Agent choices are built from its internal representation, its model of the world. The model captures what there is and how it works, thus allowing the agent to predict what would happen if it does something or not, a complete view on that from a Systems Theory perspective [Klir92] is shown in Figure.
In other words, tacit knowledge allows an agent to choose the best options that, hopefully, will help it achieve its goals. These goals are unimportant from a generic point of view. They might range from survival to booking a ticket, passing through getting a favourable transoceanic export rate, for instance.
For social agents, tacit knowledge is also stored distributed in common habits established in a community [Polanyi97,Tsoukas96]. The same principles apply, although from the perspective of the whole community as an agent. It can be also considered tacit because it is not explicitly represented in the community. It is distributed while agent act collectively, for example by imitation. This process is also known as socialisation [Nonaka95], a complete view of the tacit-explicit knowledge cycle is shown in Figure. Human natural languages are an example of tacit shared knowledge. Although a part of natural languages can be formalised, humans acquire natural language abilities mainly by imitation.
Knowledge is exchanged between social agents because this way each agent gets access to more than the knowledge it has been able to build up. Obviously, each agent, and the community as a whole, is then more prepared to make the correct choices. Agents have access to more than individual experiences and even unprecedented situations can be resolved satisfactorily.
However, tacit social knowledge is exchanged inefficiently. The exchange mechanisms, e.g. imitation, are restricted to local range. This reduces knowledge propagation in space and time.
To overcome these limitations, some agents have developed ways to make knowledge explicit and encode it in more perdurable form. Human languages are an example of this. They have written forms as perdurable encoding, always with some kind of physical support. Moreover, technology advances have also allowed perdurable encoding of languages oral form.
Other kinds of agents have developed external and perdurable knowledge formats. For instance, cells DNA can be considered an encoding of how to reproduce a cell thus allowing its perpetuation.
Generally, all these knowledge transmission mechanisms are studied by Semiotics. They are based on signs, their basic components. Signs stand for things in the agents' domain. They are the building blocks of agents' internal world models and they are encoded and transmitted during knowledge sharing. More details about Semiotics are shown in Figure and the Semiotics section.
As has been said, explicit knowledge can overcome space-time limitations of tacit knowledge exchange. Perdurable encoding and transmission mechanisms allow that it can be acquired a long time after its encoding and far away its origination point.
However, many of these representations carry interpretation ambiguities. This is because they are not wholly formalised. They are so expressive that some exchanged knowledge can be acquired at the destination leading to a different piece of knowledge.
However, this cannot be considered a bad property. Ambiguity provides easy adaptation of the representation mechanisms to new situations. For instance, metaphor produces a new interpretation of a previous representation inside a particular context. Ambiguity also allows exploration of new possibilities because knowledge is not confined in a restrictive immutable form. A good example of this advantage is DNA.
The previous risk of misunderstanding during knowledge exchange is the reason why this kind of encoded "knowledge" should not be considered knowledge. It is more appropriate to say that it is information. The encoded knowledge can be completely lost if the receiver agent cannot understand it. For instance, if two agents exchange a written message but the second one does not understand the used language, nothing of the originally codified knowledge can be retrieved.
Therefore, to be completely strict, there does not exist more knowledge than tacit knowledge. Information is the small part of it an agent is able to articulate [Stenmark02]. When an agent receives some information, it uses its tacit knowledge to interpret it and, possibly, this may lead to a change in the tacit knowledge it possesses.
However, this categorisation is in practice relaxed. There are different kinds of information and normally when the exchanged information is rich enough it is considered knowledge. Rich information has embedded enough contextual information to facilitate its full interpretation. Moreover, some encoding restrictions must be imposed in order to guarantee, to some extent, a final interpretation near to the original encoded knowledge.
In the opposite side of information rich enough to be considered knowledge, there is data. It is de-contextualised information, i.e. too distant from the knowledge required to interpret it.
As mentioned before, despite ambiguity advantages, sometimes it is necessary to exchange knowledge as reliably as possible. This has been a clear requirement in human societies for a long time. Indeed, Socrates can be considered a starting point in this formal knowledge exchange research, but roots could be extended even before.
From these remote times, humans have developed many representation formalisms. All them define their own set of shared constraints that must be incorporated as tacit knowledge in knowledge emitters and receiver. Once a formalism has been incorporated in the tacit knowledge of a community, this community can share information in a so direct and rich way that it can be considered knowledge exchange.
These formalisms can be very simple, for instance defining a set of reserved natural language words with an agreed community meaning. Then, community agents can share knowledge interchanging messages that use these agreed words. This is an example of a purely textual formalism, but there are also graphical ones. They are called diagrammatic formalisms and they are quite simple and easier to interpret, for instance Conceptual Maps [Novak84].
However, the more powerful formalisms use techniques that are more sophisticated. They are mainly based on mathematics, philosophy and cognitive science. These disciplines provide basic ideas of how we perceive and model the world. Thus, they set a base that we naturally share, although not in an obvious way.
Mathematics provides a compact set of principles widely shared among human society. This shared common base allows the construction of very powerful expressions. These expressions have clear meaning for those that incorporate the used part of the shared mathematical base into their tacit knowledge.
Meanwhile, philosophy studies the nature of knowledge, how we create and manage it. Some techniques have been developed that capture a part of our brain operation. Most of them use mathematical tools to some extent. For instance, logic and ontology are two building blocks of Knowledge Representation. On the other hand, there are also attempts to explain mathematics from a philosophical point of view [Lofting].
Despite all the possibilities of advanced representation formalism, it is important to remark that tacit knowledge is richer than any description of it.
As has been shown along the previous sections, the final objective of knowledge representations is to make knowledge explicit. Knowledge can be shared less ambiguously in its explicit form and this became especially important when machines started to be applied to facilitate knowledge management.
Nowadays, Knowledge Representation is a multidisciplinary field that applies theories and techniques from:
Therefore, Knowledge Representation can be defined as the application of logic and ontology to the task of constructing computable models of some domain [Sowa00]. Logic and Ontology provide the formalisation mechanisms required to make expressive models easily sharable and computer aware. Finally, thanks to computational resources, great quantities of knowledge expressed this way can be automated. Thus, the full potential of knowledge accumulations can be exploited. However, computers play only the role of powerful processors of more or less rich information sources. The final interpretation of the results is carried out by the agents that motivate this processing, in this case human users of the knowledge management systems.
At this point, it is important to remark that the possibilities of the application of actual Knowledge Representation techniques are enormous. Knowledge is always more than the sum of its parts and Knowledge Representation provides the tools needed to manage accumulations of knowledge and the World Wide Web is becoming the biggest accumulation of knowledge ever faced by humanity. These possibilities will be more deeply explored in the next State of the Art sections, devoted to Web Technologies and the Semantic Web.
In addition to the previous definition, Knowledge Representation can be also described by the five fundamental roles that it plays in artificial intelligence; they are the Knowledge Representation principles [Davis93]:
When applied in the computer domain, knowledge representations range from computer-oriented forms to conceptual ones nearer to those present in our internal world models. Five knowledge levels can be established using this criterion [Brachman79]:
This is one of the fundamental aspects of knowledge representation as presented in the Knowledge Representations section. Logic was developed as an attempt to create a universal language based on mathematical principles. Therefore, it is based on formal principles that impose some requirements over a knowledge representation language to be a logic:
Natural Languages can represent a wider range of knowledge, however, logic enables the precisely formulated subset to be expressed in computable form. On the other hand, although there are some kinds of knowledge not expressible in logic, such knowledge cannot be represented either on any digital computer in any other notation. The expressible power of logic includes every kind of information storable or programmed on any digital computer.
There are many logic types; each one particularly suited to its target application domains and with despair expressive capabilities and computational requirements. Logic systems vary along six dimensions from what can be considered the reference logic, First Order Logic (FOL):
System T is a version of modal logic. Each version is defined by the assumed axioms that make them more or less strong. This version assumes, among others, one important axiom:
□p → p (anything that is necessarily true is true).
For instance, this axiom used in database theory to define constraints.
Deontic logic is a weak version of Modal logic, for instance weaker than System T. It is particularly appropriate for legal domains. Modal operators are interpreted as obligation (□) and permission (◊). Moreover, the previous axiom is not applicable as laws can be violated, i.e. it is not true that anything obligatorily true is true. A weaker version of it must be assumed:
□p → ◊p (anything obligatorily true is permissibly true).
Higher-order logic is a metalanguage extension to FOL plus an ontology for relations. Thus, despite FOL quantifiers that can only range over simple individuals and names of relations and functions, HOL quantifiers can also range over relations and functions, i.e. domains of relations and functions constructed out of domains of individuals.
These can also be seen in the differences in equality theory. In first-order semantics, equality between predicates is intensional, names level, while higher-order equality is extensional, over the predicate domain. Some examples of Higher-order logics are:
Second-order logic is supplemented with an ontology for all possible relations among simple individuals.
Third-order logic includes an ontology for all relations of relations and etcetera for logics of order above.
Compared to FOL, HOL has greater expressive power but, opposite to FOL, it is incomplete [Gödel92] and thus lacks practical computable models. More about this issue is presented in the Inference section.
However, some syntactical tricks can be used in the FOL domain to enjoy some higher-order logic features. Instead of using higher-order semantics that allow variables range over relations, first-order semantics can be combined with higher-order syntax. Higher-order syntax allows variables to appear in places where normally predicate or function symbols do and, therefore, assertions about assertions are possible. Altogether, in latter instance, this is only what is informally called “syntactic sugar”. Some kind of stratified reasoning is needed to finally avoid HOL complexity. FOL-like reasoning is carried out separately for the object level and the meta-level [Kowalski86] provided by higher-order syntax.
Reification is a formal trick of this type. For each predicate, a constant that stands for it is created. These constants are used in axioms. However, since they are constants, the resulting theory is first-order. This is useful for expressing control knowledge; facts are reified so one can say when they are relevant. Reification can also be used to reify modal logic semantics and drop reasoning to first-order.
Frame logic [Kifer95] is an example of this kind of logics; it combines first-order semantics with higher-order syntax. In contrast, FOL has both first-order syntax and semantics.
To better explain the term semantics, it is going to be situated in the context of semiotics, the general theory of representations. Moreover, as altogether is used by agents, the view is going to be completed with its relation to agents from the systems point of view. This would complement the view of knowledge from systems theory presented in the Tacit Knowledge section.
Semiotics studies signs, that comprise icons, tokens, symbols, etc., and thus the complete representations range. It covers them in general: their use in language and reasoning and their relationships to the world, to the agents who use them, and to each other. Therefore, it comprises all languages, informal and formal, presented in previous sections.
Human languages are a specific case of semiotics. A language is a system of conventional spoken or written symbols by means of which human beings, as members of a social group and participants in its culture, communicate.
Formal languages, like logics, are also studied by semiotics. Logics are also based on symbols. The difference is that some restrictions are imposed on syntax and semantics. These restrictions reduce their expressiveness but also ambiguity and thus facilitate their automation.
Semiotics has three dimensions that cover specific aspects of signs:
In Figure these three terms are situated in the systems theory view of agents previously presented in the Tacit Knowledge section.
As a part of semiotics introduced in previous section, semantics deals with how knowledge representations are related by agents to the things they stand for. This description must be further detailed. At a first glance, it only captures the part of semantics that relates an agent with its environment. This facet should be complemented, as will be demonstrated soon, with a supplementary one that will complement the full range of processes where semantics are involved. These more detailed aspects of semantics are denotational and representational semantics [Chierchia00]:
Denotational - Reference: the denotational aspect is outward looking. It is the study of the relation of symbols to what they stand for in the world. Reference corresponds to the denotation and it is the extension of an expression, what it stands for on a given situation of its use.
Representational - Sense: on the other hand, the representational aspect is inward looking. It considers how contents are mentally represented and corresponds to the sense or intension of an expression. The sense is what enables us to communicate with each other. It is inter-subjective, and thus objective inside a community of users. Therefore, it is not the individual subjective mental representation. It is the information content we grasp in understanding a sentence, the meaning.
This two-sided view of semantics gives birth to the sense and reference distinction shown in the Meaning Triangle Figure.
Considering the previous distinction, an expression stands for its reference, not in all respects, but in relation to a sort of idea, its sense [Pierce35]. The sense-reference distinction allows dealing with semantics extreme cases, like multiple expressions with the same reference or expressions with non-existent reference, e.g. fiction entities.
An example of the first case is shown in Table, where other examples about more elaborated expressions are also shown.
| Expression | Reference | Sense |
| Nominal Phrases “The morning star” |
Individuals Venus |
Individual concepts The concept of the star that disappears last in the morning |
| Verbal Phrases “Is Italian” |
Classes of individuals The Italians |
Concepts The concept of being Italian |
| Sentences “Pavarotti is Italian” |
True or false True |
Thoughts The though that Pavarotti is Italian. |
The expression “the morning star” is used about the last star visible in the morning; this is the sense of the expression. However, the reference is the same as that for the expression “the evening start”, the Venus planet. On the other hand, the meaning for the later is the star that appears first in the evening.
Sentences are more complex expressions that denote a proposition or world state of affairs. Denotational semantics makes possible to determine the validity of this proposition, i.e. if the state of affairs holds or not in the current state of the world where interpretation takes place.
It must be remarked that common knowledge representation systems work at the representational level. They manage pieces of information and relate them to senses previously established by knowledge representation means. These sense definitions are mainly captured by ontologies, one of the components of knowledge representation. The other non-computational component, logic, may also capture some representational semantics as built-in ontologies.
Therefore, representational semantics operate only at the abstract level. A great part of the meaning can be captured at this level. This can be done defining concepts, conceptual relations among concepts and combining them to capture expressions that are more complex. However, to acquire its full semantics, a knowledge representation must be grounded, i.e. connected to the world.
At the denotational level, knowledge representation systems are only able to maintain truth if they use valid reasoning methods and start from valid premises, more details in next section. The denotational semantics of knowledge representation languages are also called language semantics. They describe how to compute expression interpretations from previous interpretations of their constituents. Therefore, some preliminary grounding at the starting point is needed. Moreover, if truth is not preserved by reasoning methods, further interpretation is necessary to check conclusions validity.
In order to automate the denotational level, machines must have some kind of external world sensors that allow them to relate expressions and concepts to external objects. These issues are studied applying robotics and artificial intelligence techniques and lay outside the scope of the research work captured in this memory.
Inference is what makes a logic more than a notation. Inference rules determine how one pattern can be generated from another. Thus, new pieces of knowledge can be added based on previous ones [Russell95]. The final objective is to capture how agents in general reason about what they know. There exist different kinds of reasoning and this leads to different inference types: deduction, abduction and induction.
It is also known as logical inference because deduction is the type of reasoning that logics try to capture. The more important characteristic of deduction is that it preserves truth as determined by semantics. From true premises, it guarantees a true conclusion.
Logics that support this kind of reasoning are called sound logics. More details about this are presented in Table.
| Semantic tests, stated in terms of the entailment operator ╞, provide criteria for evaluating the rules of inference. Entailment operates at the denotational level, while inference operates at the referential level. Rules of inference define the provability operator ├, i.e. that something is provable. Semantic entailment is more fundamental than provability because it derives the truth of formulas from facts about the world. Provability depends on the rules of inference of a particular version of logic, and those rules must be justified in terms of entailment. Two desirable properties of inference are: Soundness means that everything provable is true. Rules of inference are sound if provability ├ preserves truth as determined by semantic entailment ╞. (∀s:Situation)(∀p,q:Proposition)(s╞ p → (p├ q → s╞ q)). Completeness is the converse of soundness. Everything true is provable. (∀s:Situation)(∀p,q:Proposition)((s╞ p → s╞ q) → p├ q)). For FOL, the distinction between ├ and ╞ can be ignored because soundness and completeness guarantee that they are equivalent. For other versions of logic, however, they must be carefully distinguished. Kurt Gödel proved in 1931 [Gödel92] the incompleteness of higher-order logic by finding propositions entailed by ╞ that are not provable by ├. Non-monotonic logic is not even sound because it makes default assumptions. Instead of preserving truth, the non-monotonic rules of inference preserve only the weaker property of consistency: all true statements must be consistent, but not all consistent statements are true. |
These are the rules of inference for propositional logic, i.e. without quantifiers:
These ones are the inference rules for deduction with quantifiers. Together with the rules for propositional logic conform FOL rules of deduction:
Full deduction, though complete, is computationally an expensive process. Therefore, when it is implemented, some tricks are applied to make this process practical. Two general approaches are forward-chaining and backward-chaining. They consider only subsets of logic deduction.
This inference type is not a legal inference because it allows false conclusions. Abduction is an explanation generation process. Some chunks of knowledge are selected, evaluated against the problem at hand and finally packaged into a theory.
Abduction may be performed at various levels of complexity [Sowa00]:
It can be summarised as: from b ∧ a→b perhaps a, i.e. it seeks an explanation for b being true.
It is the inference process involved in learning, which tries to anticipate how things will act. From series of facts, a generalisation is concluded. Induction is not a valid inference because it does not guarantee truth. Thus, it needs retraction upon contradiction, i.e. when an instance that contradicts the generalisation is found.
It can be expressed as: from P(a), P(b),… conclude (∀x)P(x).
Another kind of inference can be considered, analogy. It is a combination of second-order induction plus deduction. However, it does not preserve truth, and, indeed, not even falsify. Yet, analogy is very useful for argumentation, scientific discovery, case-based reasoning or planning.
Analogy can be summarised as: from P(a)→P(b) ∧ R(a)→R(b) perhaps Q(a)→Q(b).
Ontology has been a field of philosophy since Aristotle and from its beginnings, it has been characterised as a study of existence, a compendium of all there is in the world.
Nowadays, it has evolved in great measure in the computer science and artificial intelligence fields. Currently, ontologies are viewed as a shared and common understanding of a domain that can be communicated between people and heterogeneous and distributed application systems. A detailed description is presented Figure.
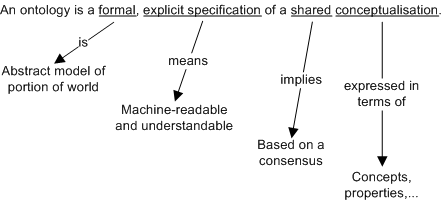
Ontology definition [Studer98]
Firstly, they were extensively used in artificial intelligence to facilitate knowledge sharing and reuse. Currently, their use is expanding to other disciplines related to information technologies. In the future, they may play a major role in supporting the information exchange processes, as they provide a shared and common understanding of a domain.
Ontologies are constructed using knowledge representation languages and logics. This allows that automatic devices make informed domain-dependent reasoning using the knowledge captured by ontologies.
As was commented in Automatic Semantics section, a great part of expressions meaning can be captured combining simpler concepts and conceptual relations, i.e. ontologies. At the end, some preliminary set of simple concepts and relations is found. This set must have a rich semantic grounding in order to make powerful and valid automatic reasoning. Moreover, if it is shared among a great community, it may permit a great level of understanding.
The kind of ontology presented in the previous paragraph is called top level or upper ontology. More details about upper ontologies are given in the Upper Ontologies section.
On the other hand, there are domain-level ontologies. They are based on upper ontologies but deal with more specific domains. Some example domains and the corresponding domain ontologies are:
Upper ontologies, also known as foundational or top-level ontologies, try to formalise the more general concepts in our conception of the world. There are many attempts to produce upper ontologies.
Many upper ontology initiatives have joined in the IEEE SUO effort (Standard Upper Ontology). One result of this working group is the SUMO ontology (Suggested Upper Merged Ontology) [Niles01]. Some of the general topics covered in the SUMO include:
The Descriptive Ontology for Linguistic and Cognitive Engineering (DOLCE) [Gangemi02] is another upper ontology that has a clear cognitive bias, in the sense that it aims at capturing the ontological categories underlying natural language and human commonsense.
DOLCE is based on a fundamental distinction between enduring and
perduring entities, i.e. continuants and occurrents, a distinction motivated
by our cognitive bias.
Classically, the difference between enduring and perduring entities is
related to their behaviour in time. Endurants are wholly present, i.e. all
their proper parts are present, at any time they are present. Perdurants, on
the other hand, just extend in time by accumulating different temporal
parts, so that, at any time they are present, they are only partially
present, in the sense that some of their proper temporal parts, e.g. their
previous or future phases, may be not present. E.g., the piece of paper you
are reading now is wholly present, while some temporal parts of your reading
are not present any more.
In DOLCE, the main relation between endurants and perdurants is that of participation: an endurant "lives" in time by participating in some perdurants. For example, a person, which is an endurant, may participate in a discussion, which is a perdurant. A person's life is also a perdurant, in which a person participates throughout its all duration.
LRI-Core [Breuker04] is a core ontology that covers the main concepts that are common to all legal domains. These domains have a predominant common-sense character and typical legal concepts such as norm, role, responsibility, contract, etc. have a grounding in abstract common-sense conceptualizations. This common sense grounding is lacking in various upper or foundational ontologies developed thus far.
One of the most important design principles that follows from the common-sense stance in developing the LRI-Core is cognitive plausibility. From this perspective, knowledge about the physical world, with the central notions of object and process is taken as a basis for a mental and abstract worlds. The intentional stance that differentiates the physical world from the mental world is also the basis for the creation of a behavioural world of roles. In summary, LRI-Core starts with four main categories: physical concepts, mental concepts, roles, and abstract concepts. A fifth category consists of terms for occurrences, which are used to talk about instances (situations) in a generic way.
Knowledge representation comprises logic, ontology and computation. Previous sections have centred on the first two components. At most, computation has been considered in relation to complexity issues. This section considers knowledge representation as a conjunction of these three components. Different implementations, i.e. conjunctions of logic, ontology and computational resources, are presented. These implementations are the last step towards putting knowledge representation into practice.
The most relevant feature of logic programming technologies is that they implement restricted versions of logic to improve performance. Generally, they use backwards-chaining implementation of inference.
Logic programming has evolved from research on theorem provers. Theorem provers use full first-order logic and implement Robinson's resolution rule, a complete and sound form of backward-chaining deduction. They are used mainly for mathematical and scientific problems.
On the contrary, logic-programming languages are used when greater performance is needed. They usually sacrifice completeness to reach this goal. However, both approaches are based on backward chaining a thus best suited to question answering.
It is a widely used logic programming language. It imposes some restrictions to its logic component. Horn-clause logic is used so it has not disjunction (∨) in implication (→) conclusions. Moreover, there is no negation in Prolog. However, it is supported at the metalevel by negation as failure. When something cannot be demonstrated with what is known, it is considered false:
Negation as failure: if fail to find answer assume falsehood, (∀x)P(x) ≡ ¬(∃x)¬P(x).
The inference mechanism is not complete. It implements backward chaining with depth first search. When the search is trapped in a cul-de-sac, backtracking is applied, i.e. last steps are undone until a new search path.
Finally, Prolog incorporates some built-in predicates and functions that provide useful primitives and non-logical programming facilities, e.g. computer input/output management. They are the facilities and building blocks over which logic programs and personalised predicates and functions are defined. They conform the ontology that captures the knowledge structures the Prolog knowledge base over which logic programs work.
Like programming languages, production systems use implication as the primary representation element. They operate with a forward chaining control structure that operates iteratively. When the premises of an implication, known as rule, are satisfied by facts in the knowledge base, it is fired. Therefore, they are particularly suited to model reactive behaviours. An example of production system rule is presented in Table.
Production System rules example
| not carrying ∧ nearby(x) ∧ grain(x) → pickup(x) ∧ carrying(x) ∧ moveRandom carrying(x) ∧ nearby(y) ∧ grain(y) → drop(x) ∧ not carrying(x) ∧ moveRandom |
Firing a rule results in interpreting its consequents. They are interpreted as actions and not as mere logical conclusions. These actions, among others, comprise knowledge base insertions and deletions. Some production systems have mechanisms to resolve cases where many rules can be fired simultaneously. For instance, the may resolve them implementing rule precedence or a non-deterministic selection behaviour.
Jess is production system implemented with Java. It is inspired in a previous production system called CLIPS. Jess implements a rete algorithm to improve rule-matching performance, the most important aspect of this kind of knowledge representation systems. In short, the algorithm maintains pointers to partial rule matches from data elements. This directly relates rules to data whose changes might affect them. Therefore, when some data is changed, it is quite direct to know which rules might then get all their firing conditions satisfied.
They are particularly suited to model static world knowledge. World objects and classes of objects are modelled as graph nodes and binary relations among them are captured as edges between nodes. There are different types of edges. Remarkably, a special type of edges defines taxonomical relations between nodes, i.e. subsumption of classes and object-class membership.
The taxonomy supports a built-in fast inference method, inheritance, to reason about generic and specific object features. The general graph structure can be used to efficiently reason about inheritance and to locate information.
Their greatest problem has been that they have lacked consensus semantics for a long time. Currently, they have been completely formalised as a subset of FOL.
The HTML language of World Wide Web can be viewed as constructing a global Semantic Network, with pages, links between pages and very limited set of link types. The only distinction is between the external link <a href=”…”>…</a> and the link to embedded images <img src=”…”>.
Frames are an evolution of semantic networks. They add procedural attachments to the node and edge structure of semantic networks. Altogether, the resulting framework and modelling paradigm has evolved into the object oriented programming paradigm.
This new paradigm has had great acceptance, for instance Sun's Java object oriented programming language. Objects and classes are nodes and relations are modelled as object references stored in object and class variables. The taxonomical relations are built-in in Java language. Subsumption is declared as “subclass extends class” constructs in class definitions. Object-class membership is stated when a new object is created with the “object = new Class” construct. The procedural attachments are represented as class methods. Their behaviour is defined with the procedural part of Java in class definitions.
They are a formalisation of Semantic Networks that allows them to be seen as sub-languages of predicate logic. They are considered an important formalism unifying and giving a logical basis to the well-known traditions of frame-based systems, semantic networks and object-oriented representations.
Special emphasis is placed in concept definitions, roles and taxonomy building constructs. Concepts describe the common properties of a collection of individuals and roles are interpreted as binary relations between objects.
Description Logics allow specifying a terminological hierarchy using a restricted set of first order formulas. Restrictions make that Description Logics usually have nice computational properties. They are often decidable and tractable, or at least seem to have nice average computational properties, but the inference services are restricted to subsumption and classification.
Subsumption means, given formulae describing classes, the classifier associated with certain description logic will place them inside a hierarchy. On the other hand, classification means that given an instance description, the classifier will determine the most specific classes to which the particular instance belongs.
Each description logic defines also a number of language constructs, such as intersection, union, role quantification, etc., that can be used to define new concepts and roles.
Fast Classification of Terminologies (FaCT) is a Description Logic classifier. The FaCT system includes two reasoners, one for the description logic SHF (ALC augmented with transitive roles, functional roles and a role hierarchy) and the other for the logic SHIQ (SHF augmented with inverse roles and qualified number restrictions). Both of them are implement using sound and complete tableaux algorithms. This kind of algorithms is specially suited for subsumption computation and has become the standard for Description Logic systems [Horrocks98]. More details about different description logics are presented in Figure.
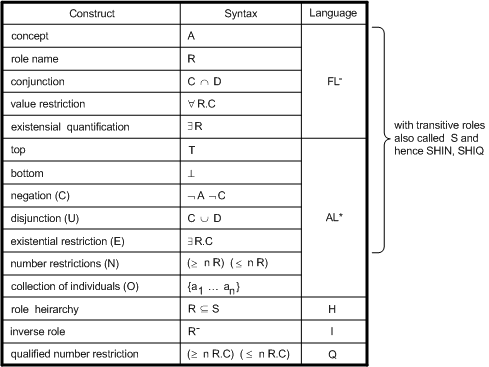
Description Logics languages and their characteristics, from [Reynolds01]
Conceptual Graphs were developed from Existential Graphs [Peirce09] and Semantic Networks. They are under standardisation process [Sowa01] in conjunction with KIF (Knowledge Interchange Format) [Genesereth98]. Both are different ways of representing FOL. KIF is an attempt to standardise a linear syntax of FOL while Conceptual Graphs provide a diagrammatic syntax. A comparative of them is presented in Figure and Table.
KIF and FOL equivalent representations for the example conceptual graph in Figure
| exists ((?x Go)(?y Person)(?z City)(?w Bus)) (and (Name ?y John) (Name ?z Boston) (Agnt ?x ?y) (Dest ?x ?z) (Inst ?x ?w))) (∃x:Go)(∃y:Person)(∃z:City)(∃w:Bus) (name(y,'John') ∧ name(z,'Boston') ∧ agnt(x,y) ∧ dest(x,z) ∧ inst(x,w)) |
Although Conceptual Graphs are equivalent to FOL, their graph orientation provides many features that make them especially useful. They express meaning in a form that is logically precise, humanly readable, and computationally tractable. With a direct mapping to language, conceptual graphs serve as an intermediate language for translating computer-oriented formalisms to and from natural languages. With their graphic representation, they serve as a readable, but formal design and specification language.
Moreover, there have new inference facilities. Existential Graphs provide a more simple set of rules to perform deduction. Other kinds of inference are also benefited. Graph structure can be used to implement efficient algorithms to reason with analogy [Leishman89].
When finally Knowledge Representation is put into practice by applying knowledge representation technologies, two disciplines can be considered: Knowledge Engineering and Knowledge Management.
It is a terms that refers to Knowledge Representation used for some purpose. Its relation to knowledge representation can be compared to the relation of Mathematics or Physics to Engineering.
It is a broad discipline that usually involves Knowledge Representation techniques. It ranges people, organisational processes, business strategies and Information Technologies. Knowledge Management could be defined as the development of best practices to add value to a company through maximum use of the data, information and knowledge within. It should also harness potential knowledge and tacit knowledge, with the intention of converting them into explicit knowledge, to be then made accessible as shareable and re-usable company assets.
Information Systems process information without engaging the users. Knowledge Management Systems help users understand information and, contrary to Information Systems, they include users perspective, i.e. the relation between the piece of information and users knowledge. This includes the situation where the user develops the information need and the analysis of the usage of the same information once it has been obtained and interpreted by the user [Alavi01].